【例题1】

　　10级阶梯，每次可以登上1级或者2级，请问有多少种走法?

　　【解析】我们先一步步看。假设要上第一级阶梯，其方法数S1=1。假设要上第二级的阶梯，要么一级一级走，要么一次走两级，故其方法数为S2=2。上第三级阶梯，其方法可以分成两类：最后一步走1级和最后一步走两级。如果确定最后一步走一级，即只需要算出走到第二级阶梯的方法数,即S2。如果确定最后一步走两级，即只需要算出走到第一级阶梯的方法数,即S1。故S3=S1+S2。同理如果要上第4级阶梯，S4=S2+S3。依次类推，我们可以得到一个一般性公式，Sn=Sn-1+Sn-2。按照该公式，可列表如下：　　

　　【例题2】

　　如图所示为两排蜂房，一只蜜蜂从左下角的1号蜂房到8号蜂房，假设只向上或者右爬行，则不同走法有几种?　　

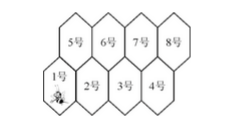
　　【解析】到5号蜂房的方法数S1=1，到2号蜂房有两种方法：1-5-2或者1-2，记S2=2 。到6号蜂房分成两类：最后一步从5到6和最后一步从2到6，记到6号蜂房方法数为S3，得到公式S3=S1+S2。后面的蜂房也可以按照相同的方式类推，最终得到公式Sn=Sn-1+Sn-2，故其结果如下：　　

　　因此，最终答案为21。

　　【例题1变形】

　　10级阶梯，每次可以登上1级或者3级，请问有多少种走法?

　　【解析】上1级阶梯，方法数S1=1，上2级阶梯只能一级一级上，方法数S2=1。上三级阶梯有两种情况：一次上三级或者一级一级上，故方法数S3=2。上四级阶梯，分成两类：最后一步走一级和最后一步走三级，若确定最后一步走一级，只需要算出到第三级阶梯的方法数。最后一步走三级，只需要算出到第一级阶梯的方法数，得到公式：S4=S1+S3。依次类推，最终可得到公式：Sn=Sn-1+Sn-3，得结果如下：